Specificaties nameten

Uit vele voorbeelden op internet blijkt dat vooral in de goedkopere klassen, maar ook onder middenklasse kijkers, er aardig wat modellen zijn te vinden, waar de specificaties niet van kloppen. Het is niet al te moeilijk om verrekijkereigenschappen, zoals vergroting, uittreepupil, effectieve objectiefdiameter en beeldhoek zelf na te meten. Je kunt je afvragen of dat nuttig is. Als je tevreden bent met je kijker geeft het wellicht alleen maar een teleurstellend gevoel als na meting blijkt dat diameter en vergroting kleiner zijn dan gedacht, en pak je de kijker met minder plezier weer op. Wat schiet je er mee op?
Tja, zelf ben ik gewoon nieuwsgierig. Bovendien ben ik me er graag van bewust, als iemand me beduvelt. 

We bekijken achtereenvolgens de effectieve objectiefdiameter, de uitreepupil/vergroting, het (ware) beeldveld en het schijnbare beeldveld.
 

Meten effectieve objectiefdiameter.

De objectiefdiameter kun je natuurlijk met een liniaal simpel meten aan de buitenkant. Dit komt bijna altijd wel overeen met de specificaties. De adder onder het gras is, dat achter de lens afschermende diafragmaringen kunnen zitten, en/of de prisma’s die (te) klein zijn, zodat de kijker niet de volledige opening benut. Daarom willen we de effectieve objectiefdiameter weten: de diameter van het deel van de voorste lens die de kijker echt gebruikt om een beeld te vormen. 

De effectieve objectiefdiameter kun je meten door de volgende stappen uit te voeren in een redelijk donkere kamer:

• Stel de verrekijker scherp op oneindig (ver weg is scherp).
• Richt een slanke led-zaklamp op een afstand van 25 à 30 cm op het oculair, zo dichtmogelijk op de optische as.
• Plaats een wit vel en een liniaal dicht op het objectief en meet de diameter van de geprojecteerde lichtcirkel, zoals die op de liniaal wordt geworpen.

Op de afbeelding meet ik als praktijkvoorbeeld een 10x50 verrekijker door. De effectieve objectiefdiameter blijkt 46mm. Dat is significant kleiner dan de 50mm die op de kijker staat vermeld!

Meten uittreepupil en vergroting

Om de vergroting van de verrekijker te bepalen gaan we de uittreepupil meten, want:

Vergroting = Effectieve objectiefdiameter ÷ diameter van de uittreepupil

De uittreepupil is klein, dus een kleine meetfout geeft al gauw een verkeerde waarde. We willen op een tiende van een millimeter nauwkeurig meten. Met een schuifmaat en eventueel een loupe is dat goed te doen. Maar makkelijker is het, vind ik, om een foto van de uittreepupil te nemen, samen met een liniaal. In een fotobewerkingsprogramma leg ik vervolgens de liniaal over de uittreepupil en vergroot het beeld.
Bij de “10x50” meet ik een uittreepupil van 5.0mm. 
De vergroting is dus 46mm ÷ 5mm = 9,2. 
 

Als je de effectieve objectiefdiameter niet hebt gemeten, dan kun je forceren dat je die wel weet: dek het objectief af met een ring met een opening van (bijvoorbeeld) 35mm - je diafragmeert de opening - en meet de uittreepupil nogmaals. .

De vergroting van de kijker verandert niet als je diafragmeert. De uittreepupil zal kleiner zijn (tenzij je diafragma groter is dan de effectieve opening).

De werkelijke gemeten vergroting berekenen we uit de kijkerhelft met het diafragma: 

Gemeten vergroting = 35mm ÷ 3,9mm = 9,0 x

We hebben dus te maken met een 9 x 45 verrekijker, en geen 10 x 50!

Het (ware) beeldveld meten

Als je door een verrekijker kijkt, dan is de volledige cirkel met wat je ziet het beeldveld. De grootte van de het beeldveld is een belangrijke eigenschap van de kijker. Hoe groter het beeldveld, hoe groter het deel van de sterrenhemel je kan vangen in één beeld.  We drukken de grootte van het beeldveld uit in het aantal graden dat de diameter van het beeld bestrijkt. Tussen de 5 en 8 graden is een normale waarde voor een gewone verrekijker.

De grootte van het beeldveld staat altijd vermeld in de specificaties die de fabrikant opgeeft. Meestal staat het zelfs op de verrekijker zelf. Maar klopt dat altijd? Zo had ik direct twijfels over de aangegeven 8,1 graden van mijn 8x42 Bynolyt Runner III. 

Er zijn verschillende methodes om de grootte van het beeldveld te meten. We lopen er een paar langs, zodat je kan kiezen wat bij je past.

Sterveld bekijken
Als je twee sterren hebt die nét in je beeldveld passen, dan is de hoekafstand aan de hemel tussen die twee sterren ook de hoek van je beeldveld. 
Een super simpele methode, maar je hebt wel een heldere hemel nodig. En vind dan die geschikte sterren maar eens. In de gratis app ‘Sky Chart / Cartes du Ciel’ kun je hoekafstanden tussen objecten opvragen, dat is een handige hulp hierbij.

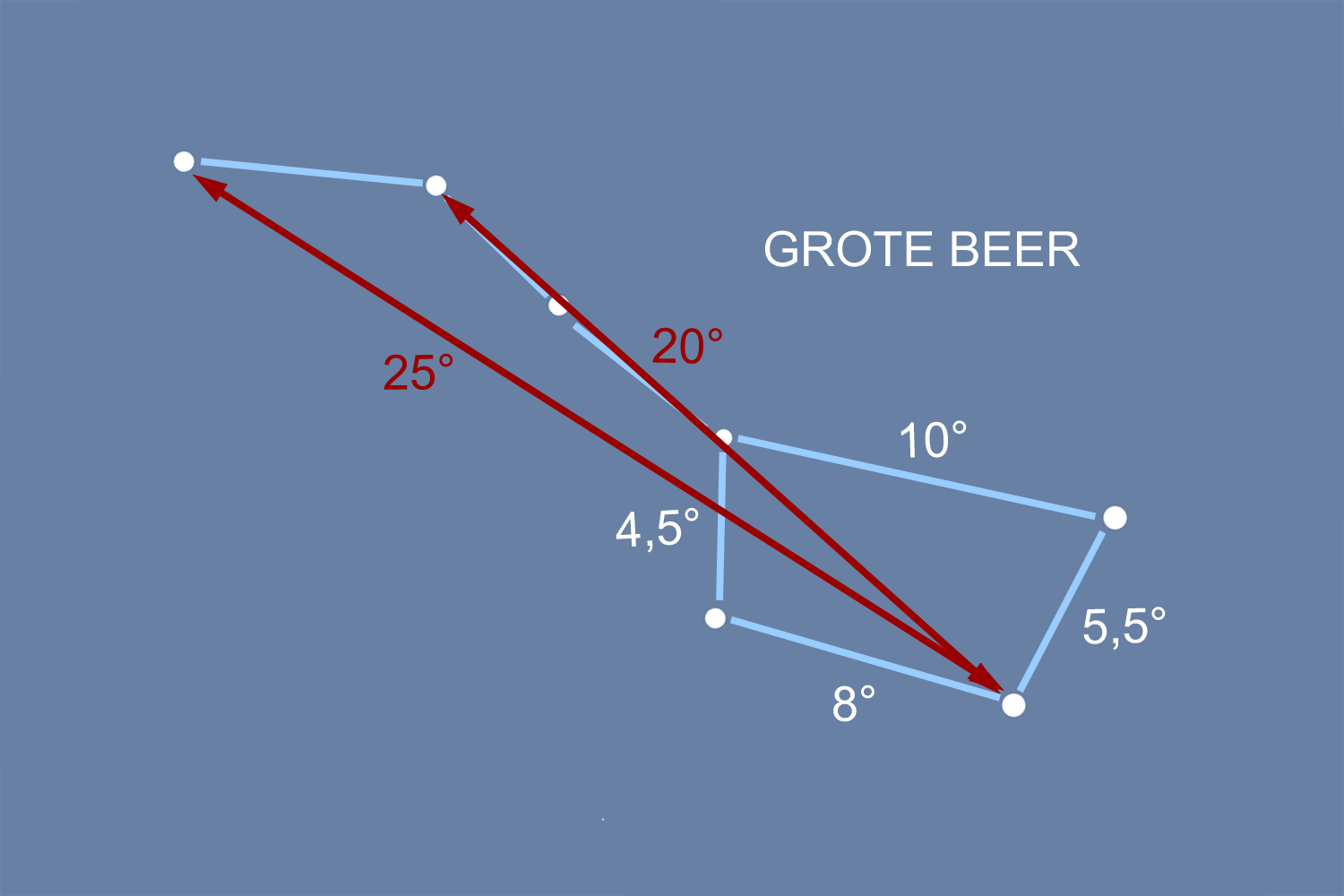
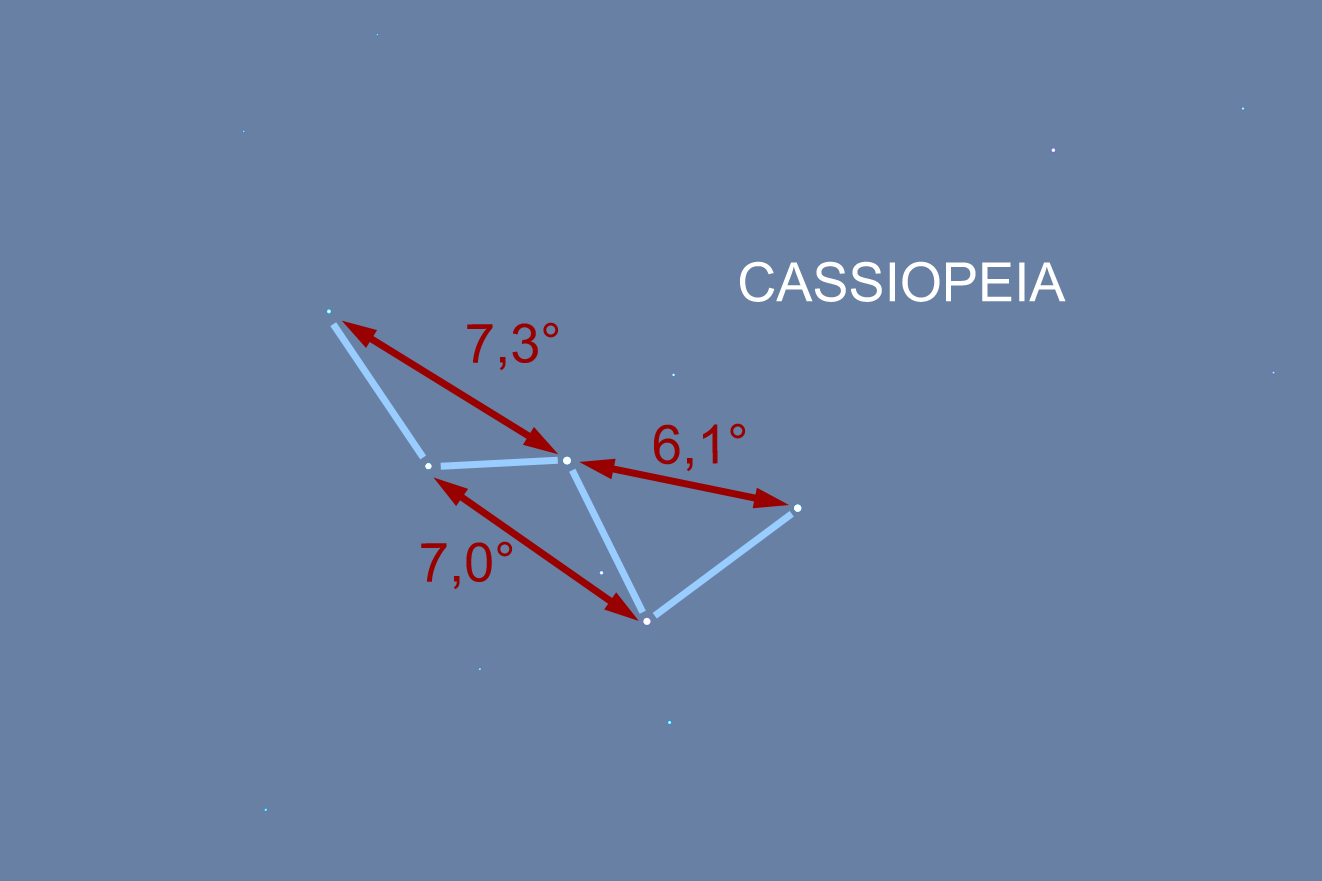
Voor een eerste indicatie geef ik je enkele hoekafstanden in de Steelpan en Cassiopeia:

Driften (wegdrijven)     
Een nauwkeurige methode is de drift-methode. Als je het goed uitvoert kun je het beeldveld tot op de tiende graad nauwkeurig meten.

• Zet de kijker op een statief en richt op een ster in zuidelijke richting die nabij de hemelequator staat.
• Heb je zo’n ster gevonden, dan beweeg je de kijker heen en weer in oost-west richting en je zet de hoogte van de kijker dusdanig, dat de ster door het midden van het beeld heen en weer beweegt.
• Zet nu de ster op de linker rand van je beeldveld (de oostkant), zó dat je de ster net niet ziet. Beweeg de kijker nu niet meer!
• Door de draaiing van de Aarde (of hemelbol, net hoe je het bekijkt) zal de ster na korte tijd het beeldveld in bewegen. Noteer het tijdstip.
• De ster zal langzaam het beeld doorlopen in een tempo van ¼ graad per minuut. Neem een kwartier pauze.
• Hou de ster in de gaten en noteer het tijdstip dat de ster aan de westkant het beeld verlaat. 
• Met het meten van de tijdsduur die het gekost heeft om de ster door het beeld te laten lopen weet je nu het beeldveld. Deel het aantal gemeten minuten door vier (of het aantal seconden door 240). 
  Voorbeeld: als de ster in 20 minuten het beeld heeft doorlopen is het beeldvel 20 ÷ 4 = 5 graden.

Het nadeel van deze methode is dat je op een heldere avond moet wachten + je hebt een statief met adapter nodig+ je moet je kunnen oriënteren aan de sterrenhemel + er moet een goede ster voorhanden zijn + je moet geduld hebben + de kat van de buren (en jij zelf ook niet) moet niet tussendoor tegen het statief stoten. Dit laatste verzin ik niet, het is me overkomen! 

Digitale waterpas-methode

Makkelijker is het als je een goede digitale waterpas(-app) hebt:

• Zet de kijker op een statief en richt je op een object ver weg. Zet een herkenbaar punt (bijvoorbeeld de punt van een kerktoren) helemaal onder in je beeld, op het randje.
• Meet de hoek die de kijker afwijkt van waterpas en onthoud of noteer deze.
• Richt de kijker nu dusdanig dat het herkenbare punt op het randje boven in het beeldveld van de kijker staat. 
• Meet welke hoek de kijker nu afwijkt van waterpas. 
• Trek de twee gemeten hoeken van elkaar af: dit is de hoek van je beeldveld.

Op deze manier kun je een nauwkeurigheid bereiken van een paar tienden van een graad. Je kunt ook een gradenboog gebruiken om de hoeken te meten, maar het is een uitdaging om dat met de nodige precisie te doen. 

Driehoeksmeting

Voor wie een klein beetje wiskunde/rekenen niet schuwt is er een eenvoudigere en prima uit te voeren en redelijk nauwkeurige meetmethode:

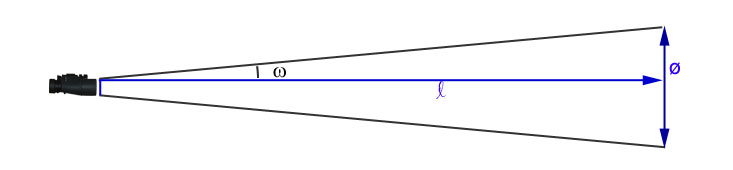
• Plaats een meetlat of (deels) uitgerolde rolmaat op een flinke afstand (zeg vijf tot tien meter) van je verrekijker. Je moet loodrecht op de meetlat/rolmaat kijken en zorg dat je de afstand meetlat/rolmaat <==> verrekijker op de centimeter nauwkeurig weet. We noemen deze afstand: l
• Kijk door één kijkerbuis, stel scherp op de meetlat/rolmaat, en lees af hoeveel centimeter je over het midden van het beeld maximaal kan zien. Deze afstand noemen we: ø
• Bereken je beeldveld:
  Beeldveld = 2w ≈ 2arctan(½ø/l)

(In de formule moeten we eigenlijk rekening houden met de diameter van het objectief. Door dit te negeren overschatten we het beeldveld. Een tweede factor die van invloed is, is dat je scherp stelt op de meetlat in plaats van op oneindig, waardoor het beeldveld iets kleiner wordt. Op een afstand van 5 á 10 meter heffen deze twee genegeerde zaken elkaar ongeveer op. Dat geeft ons de mogelijkheid om de formule simpeler te houden dan de theoretische juiste formulering.)

Terugkomend op de Bynolyt Runnr III: bij deze kijker mat ik een beeldveld van 7,3 graden in plaats van de gespecificeerde 8,1 graden. Een aanzienlijk verschil!

Het schijnbaar beeldveld meten

Het schijnbare beeldveld is de hoek van het vergrootte beeld zoals het in je oog wordt geprojecteerd. De waarde van deze hoek is ruwweg de hoek van het ware beeldveld, dat we hiervoor hebben bestudeerd, vermenigvuldigd met de vergroting. Een waarde tussen de 50 en 70 booggraden is normaal. Het is naar mijn mening minder interessant om de precieze grootte van het schijnbaar beeldveld te meten en te controleren. Sommige fabrikanten specificeren an het schijnbare beeldveld niet eens.
Toch is het grappig en leerzaam om de grootte van het schijnbare beeldveld inzichtelijk te maken: kijk verkeerd om door een verrekijkerhelft naar een object in de verte, dus kijk in het objectief naar het verkleinde beeld. Zet een herkenbaar punt aan de rand en beweeg de kijker dusdanig dat het herkenbare punt aan de andere kant aan de rand komt te staan. Je zal zien dat je de kijker een flink eind moet draaien. Die draaihoek is de hoekgrootte van het schijnbare beeldveld.

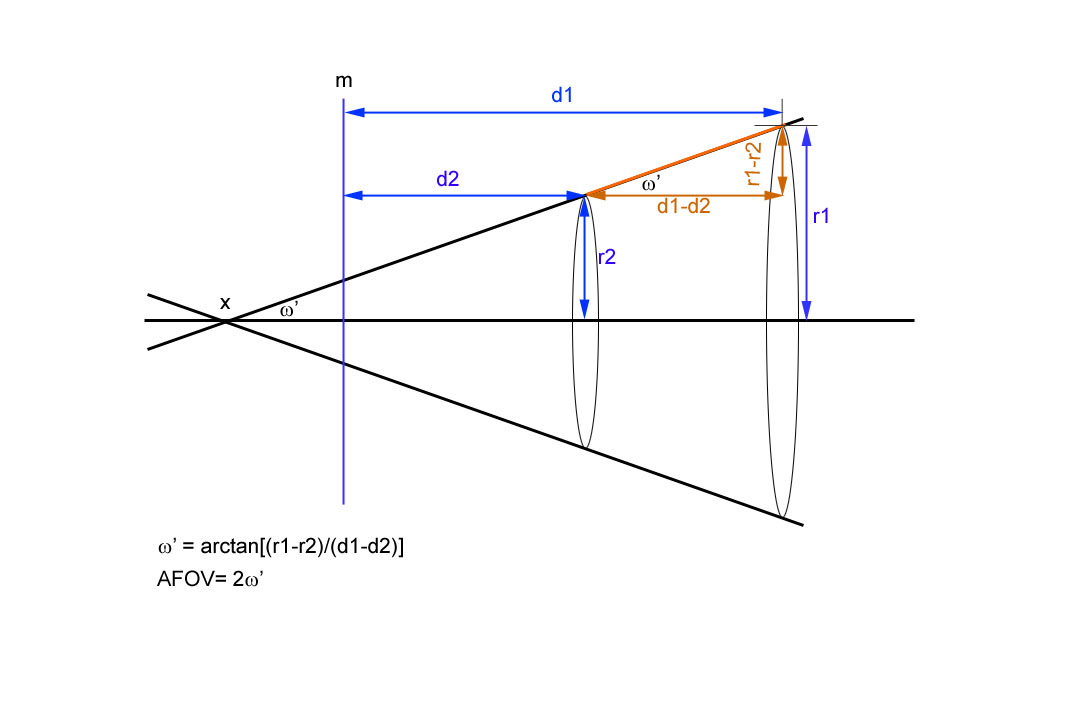
Een andere wijze om de hoekgrootte van het schijnbare beeldveld te meten is via een projectie-methode, waarbij je met een zaklamp in het oculair schijnt en de straal r (halve diameter) van de geprojecteerde bundel, op bijvoorbeeld een witte muur, opmeet. Doe dit op twee afstanden d van de muur.  De schijnbare hoek (Engels Apperant Field Of View, APOV) volgt uit wat wiskunde en rekenwerk.